Spis treści
Co to jest funkcja?
Funkcją w matematyce nazywamy pewne przyporządkowanie. Chodzi o przyporządkowanie każdemu elementowi jednego zbioru dokładnie jednego elementu drugiego zbioru.
Prosty przykład:
Dzieci w klasie mają swoje numery w dzienniku. Uczniowie reprezentują jeden zbiór, a numery z dziennika drugi zbiór. Zakładając, że Jan Kowalski ma numer 7, powiemy, że funkcja (Jan Kowalski) jest przyporządkowana do numeru 7 w dzienniku. Zapis wyglądałby następująco:
- funkcja (Jan Kowalski) = 7
Sposoby przedstawiana funkcji
Tę samą funkcję można przedstawić na kilka sposobów. Za pomocą:
- grafu,
- opisu słownego,
- tabeli,
- wykresu,
- wzoru.
Przy czym tabele, wykresy i wzory stosuje się dla wartości liczbowych.
Posiadając wzór funkcji, można już przedstawić ją na wykresie czy w tabeli. Wzory są najpowszechniejszym sposobem przedstawiania funkcji. Zapisuje się je na dwa sposoby:
- y = wzór (np. x + 2) lub
- f(x) = wzór np. x + 2.
Jakie są rodzaje funkcji w matematyce?
W różnych sytuacjach można wykorzystywać inne funkcje. Program szkoły ponadpodstawowej obejmuje w różnym zakresie następujące funkcje:
- funkcję liniową,
- funkcję kwadratową,
- funkcję wykładniczą,
- funkcję logorytmiczną.
Funkcja kwadratowa. Najważniejsze informacje:
- funkcja kwadratowa to taka, w której występuje x²,
- wykresem funkcji kwadratowej jest zawsze parabola,
- w funkcji kwadratowej oprócz potęgi może wystąpić x lub/oraz liczba stała. Wzór na funkcję kwadratową może wyglądać na przykład tak: f(x)=(x+6)2+1 lub tak: f(x)=x2+2x−1,
- wzór funkcji kwadratowej: f(x)=ax2+bx+c, gdzie a, b i c to wartości liczbowe,
- wzór funkcji kwadratowej najprościej jest zapisywać w jednej z trzech postaci: ogólnej, kanonicznej lub iloczynowej.
Wykres funkcji kwadratowej
Funkcję kwadratową przedstawia parabola. Ten rodzaj wykresu może wyglądać tak:
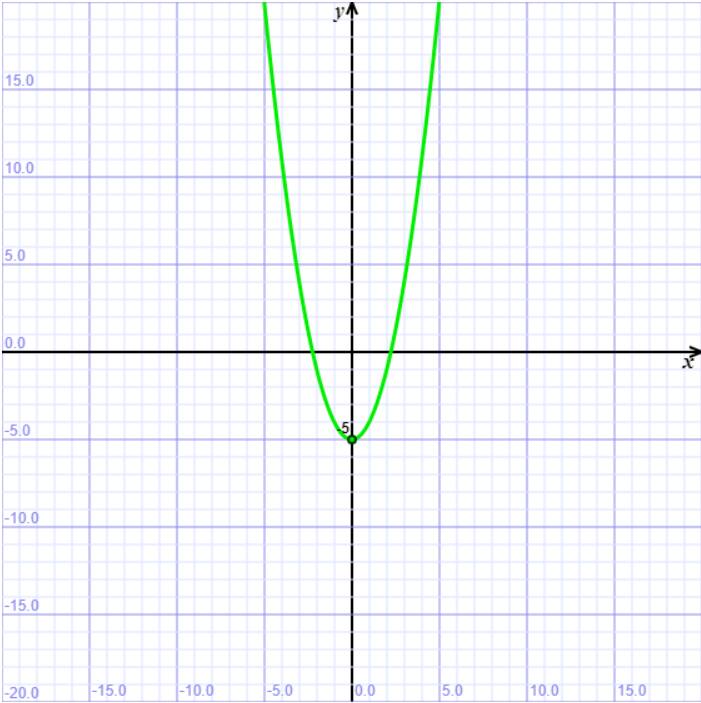
- dla f(x) = x^2 - 5
Edukacja
Ramiona paraboli są skierowane do góry, ponieważ funkcja jest dodatnia. Gdyby była ujemna, ramiona skierowane byłyby do dołu. Wiele zadań maturalnych wymaga narysowania wykresu funkcji kwadratowej oraz podania jej własności.
Jak narysować parabolę funkcji kwadratowej?
Każda parabola ma wierzchołek oraz dwoje ramion. Aby narysować wykres funkcji kwadratowej, należy ustalić:
- czy funkcja jest dodatnia, czy ujemna (kierunek ramion),
- miejsca zerowe (jeżeli istnieją, można je określić przy pomocy cyrkla),
- punkt przecięcia z osią y,
- obliczyć wierzchołek paraboli.
Własności funkcji kwadratowej
Z wykresu funkcji można wyczytać określone dane, które nazywamy własnościami funkcji kwadratowej. Są to na przykład:
- zbiór wartości,
- miejsca zerowe,
- wartości dodatnie i ujemne funkcji,
- Punkt przecięcia z osią y,
- monotoniczność funkcji,
- różnowartościowość,
- parzystość i nieparzystość.


















